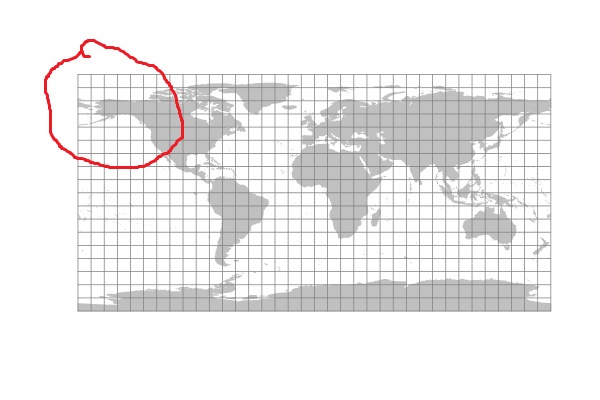
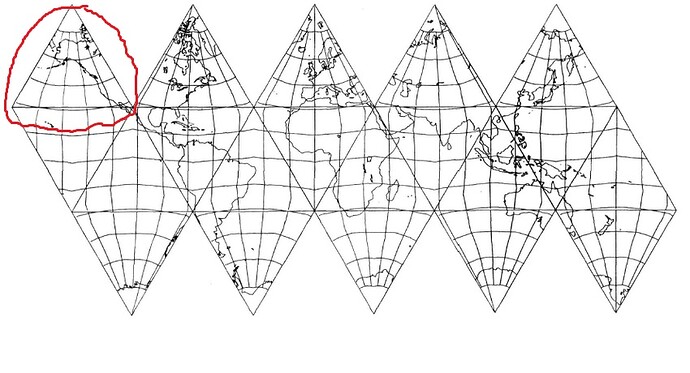
If the icosahedron is meant to be regular, then the rectangles will be squares. In this case, the triangles will be equilateral and the internal angles will all be 60°. For the top left square, what you want is to scale the lower edge by (1, 1), i.e., to leave it at its original size, the upper edge to (0, 1), i.e., it becomes a single point at the same vertical position, and the intermediate points to intermediate values for the x-value. These can be found by dividing the triangle into “bands” and finding the required width. This can be done by measuring directly or by using one of the formulae for triangle solutions (side-angle-side, etc.). Obviously, the lower limit for the height of the “bands” is 1 pixel.
The procedure is similar for the other square-triangle pairs.
If the icosahedron isn’t regular, you just have to figure out what the angles of the triangle are, which should either be known already or no problem to figure out.
So, what you need to do is to scale each band by (a, 1) for a_0, a_1 … Scaling in two dimensions by the same value in both dimensions is an affine transformation, which preserves the property of parallelity. Scaling by different values for each dimension is not an affine transformation and does not.
That being said, the easiest way to do this would be with vector data starting with a three-dimensional representation of a globe. The image you’re starting with is a cylindrical projection of a globe, probably the Mercator projection. The icosahedral mapping is similar to what one normally does for making globes, which is to make a “spherical development”. In this case, the globe isn’t divided into triangles but rather into “spherical biangles”. These plans for a cardboard model of a celestial sphere are an example: https://www.gnu.org/software/3dldf/graphics/clstsph3.pdf
It’s on this web page: The GNU 3DLDF Astronomy Page
These are some photos of a prototype: https://www.papermodelers.com/forum/751385-post23.html
It would work better, i.e., appear more spherical, with more than 8 biangles (and with less stiff paper), but this model illustrates the principle.
The easiest way to make an icosahedral model would be to project the points on the sphere onto the enclosed or enclosing regular icosahedron. However, you would need a lot of points for the contours of the continents, so unless one has this data from somewhere, it would be impractical.
Incidentally, in 3D graphics programs, 4 x 4 matrices are standard for representing the affine transformations and some non-affine transformations, such as scaling by unequal values and the perspective projection. Points are represented by “homogeneous coordinates”, which have 4 values, normally called x, y and z plus an additional w-coordinate. The latter is normally 1 but is not equal to 1 (for most points) when a point is projected using the perspective projection.