In GIMP:
Assume that I have a picture which includes an arrow that shows the length of a specific element in the picture.
I want to use the above reference to measure the length of other elements in the picture.
How is this done in GIMP?
I’m not completely certain I understand exactly what you want to do. If I am correct, one way of doing this would be to 1. make a copy of the layer including the arrow. The copy will now be the active layer. 2. Select the arrow, invert the selection and make everything else in the layer transparent. 3. Put this layer over all other layers. 4. Shift it around with the “move layer” tool, rotate it, and or transform it in any way you want using the appropriate menues.
This should work pretty well for straight lines. Please note that finding the lengths of curves, with the exception of circular arcs, is an advanced topic and there’s no solution for the general case, in GIMP or any other graphics software. Depending on the software, if curves are represented as Bézier curves or non-uniform rational B-splines (NURBS), which are the standard way of representing curves in graphics software, it may be possible to calculate an approximation using the sum of the segments. However, this is likely to be a poor approximation unless the curve is first broken up into many segments (and even then not so great).
Use the measure tool to measure the arrow in pixels:
From this you can deduce the pixel/unit ratio of the image. You set this in Image > Print size:
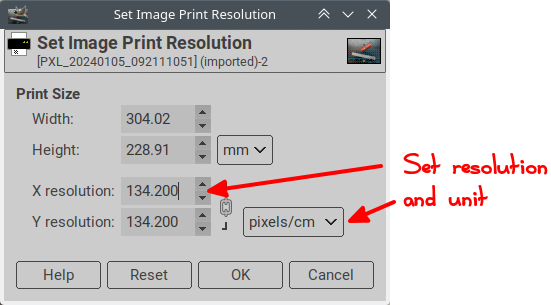
You can then set the unit indicator of the measure tool to your unit and check on the reference that you get the expected measure:
You can then get use the measure tool to measure other things:
However this is fraught with peril:
-
You have to make sure that everything is in a plane perpendicular to the camera axis (no perspective distortion)(*). On the picture parallel lines should be parallel (which is where the markings on my bench are useful, otherwise you can also use squared paper)(*).
-
You have to measure things that are the same level as the reference. As you can see in the picture, the top of the spirit level appears bigger than the base. Due to the short focal length of the camera, the smartphone was held 20cm above the bench and the spirit level is 5cm high… This would have been much less of a problem if the picture had been taken from much farther away with a telephoto lens.
(*) It may be possible to apply Gimp’s perspective correction to fix this. But if it is easy to fix the angles, you need some reference to fix the image aspect ratio, so you need two orthogonal references in the image.
If you use paths, there is a Gimp API to get their length, and I have a script that uses the API to display said length (and other information) to the user.
Thank you for the information. I made a start on reading up on paths in GIMP, but haven’t gotten very far yet. I usually use GIMP for graphics which I’ve made with GNU 3DLDF and MetaPost where the output is PNG. However, MetaPost can also produce SVG, so it would be natural to use this together with paths in GIMP. On the other hand, it’s not possible to turn off anti-aliasing in MetaPost except for PNG output, which makes things a little more difficult. I’ve had good results by posterizing in GIMP, but it may not be completely reliable.
I will also look into the measuring tool. Of course, it is possible to count the number of pixels and take the sum of the edges that represent a curve, but this is likely to be a poor approximation of the original curve. With algebraic curves, it’s sometimes possible to use integration, but, like I said, this is an advanced topic. I’ve been stuck on the problem of finding the lengths of elliptical arcs for years, because I haven’t found time to read and understand the (known) solution to this problem.
As you probably know, measuring lengths from photos belongs to the field of stereoscopy and requires special equipment. I think in a practical sense, the only way to minimize perspective distortion sufficiently with ordinary equipment is to use a repro stand. There will always be some distortion because of the way camera lenses work and probably only the center portion of the photo will yield acceptable results (varying with the focal length, field of view and the other parameters of the camera).
There will always be some distortion because of the way camera lenses work and probably only the center portion of the photo will yield acceptable results (varying with the focal length, field of view and the other parameters of the camera).
In practice very little since most lenses are rectilinear. In this picture (shot 'hand-held) the field of view is 13cm, from 28cm (as reported in the EXIF) using a close-up lens (Canon EF-S 35mm macro). As you can see the bench markings are quite regularly spaced on the picture:
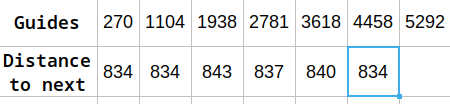
And this is a worst case, using a rather short lens, and no lens correction applied. A longer lens would imply taking the picture from further away reducing the native perspective distortion even more.
It depends on what tolerances one is working with. There’s also the question of whether the measurements are going to be used for calculations, in which case error will accumulate. If the calculations involve real numbers, or more correctly, the approximate representations of real numbers used by computers, this accumulation is likely to be significant. I can say from experience that if rotations are involved, the accumulated error is almost certain to be significant, even if one starts out with exact integer values.
The laws of linear perspective assume that the focus, which corresponds to the aperture of a camera lens, is a dimensionless point and the projection of a point in space onto the plane of projection, corresponding to the film, or the retina in the eye, is also a dimensionless point. Clearly, any real-world optical system will diverge greatly from this ideal.
corresponding to the film
In my day, cameras had film in them.
This topic was automatically closed 45 days after the last reply. New replies are no longer allowed.