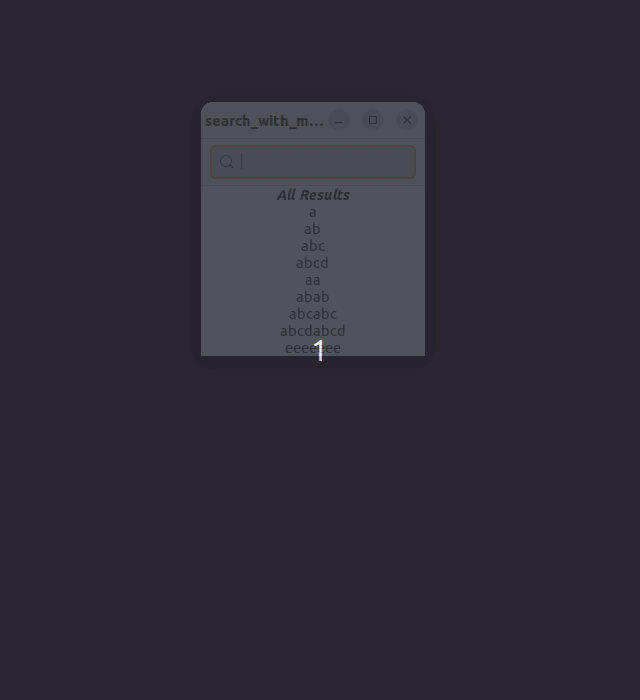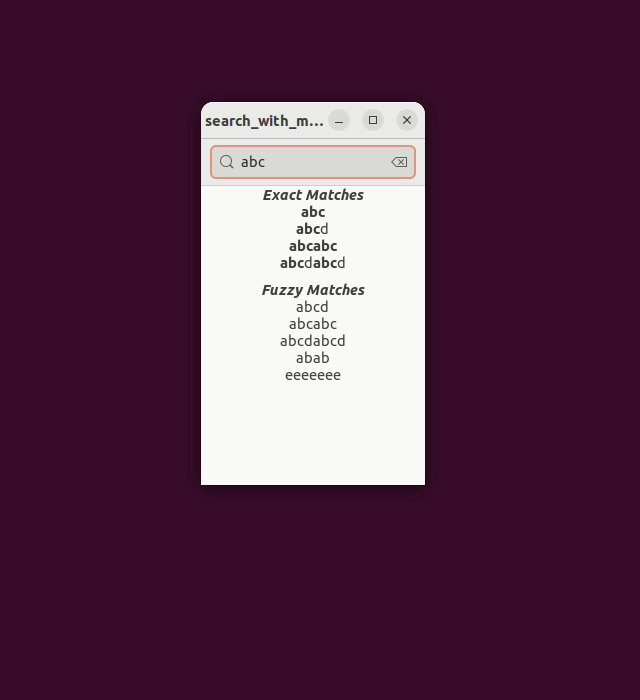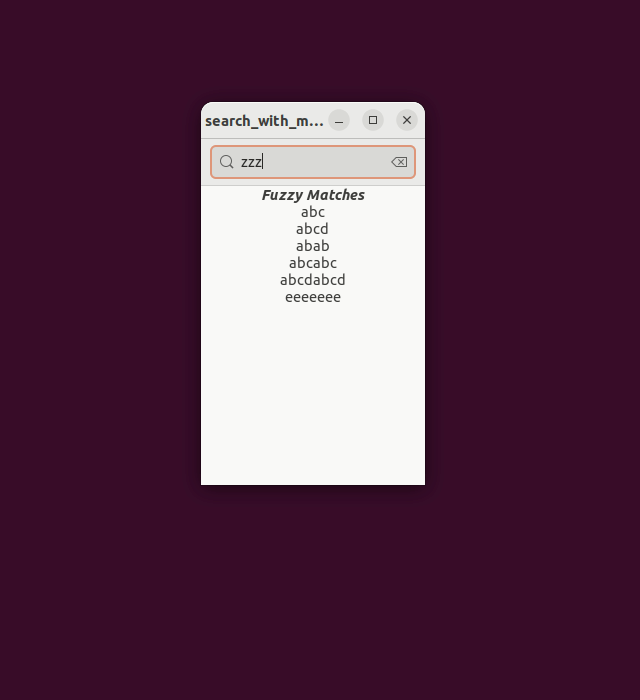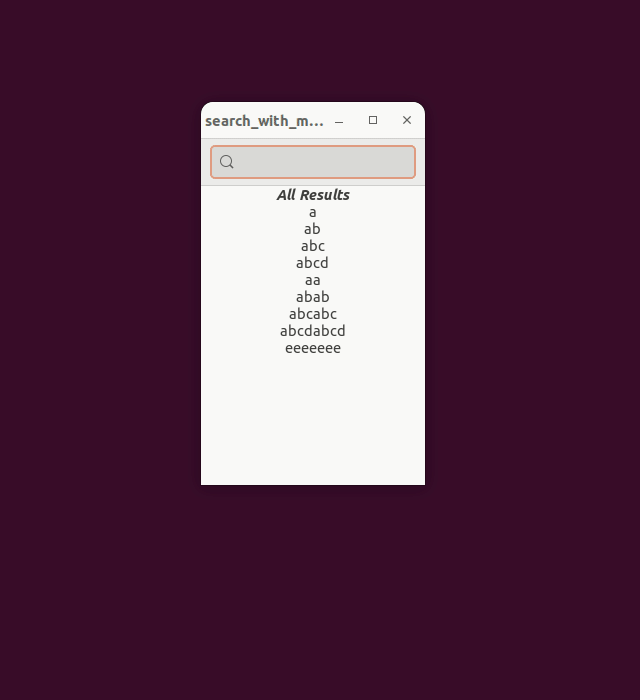
What I would like to add to GLib.
“Bitap Algorithm” fuzzy string match for strings of size:
- less than 32 characters
- less than 64 characters
What it does:
“Find the first match of pattern in string with at most k substitution errors.”
The motivation for this addition is that these are actually viable maximum sizes in many contexts, for string keys that should be searchable by the user, such as:
- image metadata tag names
- names of application settings
- names of people and places
- etc.
It would be so cool to be able to just do fuzzy search on small strings with GLib, without re-implementing it yourself, or leaning on a library which, for example, you may not want to pull into your GTK application.
The implementation of both 32- and 64-character max-length cases would be short. For the 32-character max-length case, here is a working code example. Keep in mind this is just an example. We would probably want to return an array of match objects, ordered by increasing “k” value ( the number of substitution errors ), instead of just the first match. Bitap finds every match with k or fewer substitution errors ( k=0 is exact match ). It also tells you the number of errors in a given match. These features should be fully utilized if this suggestion makes it to actual implementation.
/*
COMPILE
gcc -o bitapp bitapp.c
RUN
./bitap
*/
#include <stdlib.h>
#include <string.h>
#include <limits.h>
#include <stdio.h>
/* Find the first match of @pattern in @string with at most @k substitution
* errors.
*
* @text - The string we are searching to find @pattern.
*
* @pattern - The string we are trying to find in @text.
*
* @k - The maximum number of allowed errors. If k is zero, then the match is
* exact.
*
* @returns A pointer to the character in @text where the first match found
* starts.
*/
const char *bitap_fuzzy_bitwise_search( const char *text,
const char *pattern, int k)
{
const char *result = NULL;
int m = strlen(pattern);
unsigned long *R;
unsigned long pattern_mask[CHAR_MAX+1];
int i, d;
if (pattern[0] == '\0') return text;
if (m > 31) return "The pattern is too long!";
/* Initialize the bit array R */
R = malloc((k+1) * sizeof *R);
for (i=0; i <= k; ++i)
R[i] = ~1;
/* Initialize the pattern bitmasks */
for (i=0; i <= CHAR_MAX; ++i)
pattern_mask[i] = ~0;
for (i=0; i < m; ++i)
pattern_mask[pattern[i]] &= ~(1UL << i);
for (i=0; text[i] != '\0'; ++i) {
/* Update the bit arrays */
unsigned long old_Rd1 = R[0];
R[0] |= pattern_mask[text[i]];
R[0] <<= 1;
for (d=1; d <= k; ++d) {
unsigned long tmp = R[d];
/* Substitution is all we care about */
R[d] = (old_Rd1 & (R[d] | pattern_mask[text[i]])) << 1;
old_Rd1 = tmp;
}
if (0 == (R[k] & (1UL << m))) {
result = (text+i - m) + 1;
break;
}
}
free(R);
return result;
}
int main() {
const char *text = "hhhhhhhhhhhhereeeeeeeeeeeeeeeee";
const char *pattern = "heee";
int k = 1;
const char *a =
bitap_fuzzy_bitwise_search( text, pattern, k );
puts( a );
}
Anyways, that is what the code would look like, but less like I just stole it from Wikipedia, which I totally did. ( I can explain every line of code and how it fits into the Bitap algorithm with pictures and stuff. )
The 64-character max-length case is the same code, but with some textual substitutions:
- “unsigned long long” instead of “unsigned long”
- “63” instead of “31”.